あけましておめでとうございます。
今年は未年、ということで
マンデルブロ集合の中から羊のように見える部分を探してみました。
マンデルブロ集合とは、 Z_{n+1} = (Z_{n})^2 + C の形で表される複素数列が発散しない条件を満たす C の集合です。
シンプルな式による表現でありながらフラクタル(自己相似)であり、非常に多くの様々な形状を含んでいることが知られています。
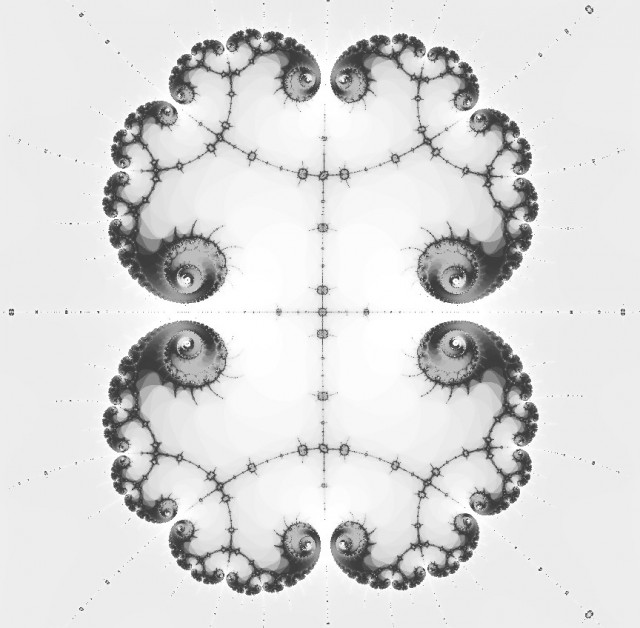
このマンデルブロ集合の中を探索してみたところ、
(x, y) = (-1.749783153, -3.355843166 × 10^(-10))
の位置から、直径約 4.573215758 × 10^(-8) の領域に、以下の図を見ることができました。
この一部を切り抜けば羊に見えるような気がしたため、
羊のような部分を切り抜いて回転させ、目を描いてみました。
なんとなく、羊のように見えると(勝手に)思っています。
数学的に美しい曲線で構成された、美しい羊です。
今年もどうぞよろしくお願いいたします。